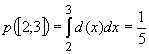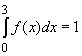Einige Lösungen der Aufgaben zu stetigen Dichtefunktionen

Lösung zur Aufgabe 2:

Es ist zwar 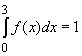, aber in Intervall gibt es negative Funktionswerte. Deshalb handelt es sich nicht um eine Dichtefunktion.

Lösung zur Aufgabe 3:

Die Bedingung 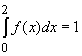führt auf . Eine Betrachtung des Graphen zeigt, dass alle Funktionswerte im Intervall positiv sind. Somit läßt sich durch geeignete Wahl von d eine Dichtefunktion erhalten.

Lösung zur Aufgabe 4:

1. Der Verlauf des Graphen legt nahe, dass es sich um eine Funktion dritten Grades handlen könnte. Sei dabei k der Funktionswert am Ende des Intervalls. Die Bedingungen    
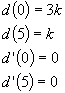
   führen auf: . Damit es sich um eine Dichtefunktion 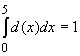handelt, muss zusätzlich die Bedingung erfüllt sein. Diese Bedingung führt auf . Also ist
2. 

zurück