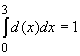 . Der Graph ist eine nach unten
geöffnete Parabel, die die x-Achse bei –3 bzw. 3 schneidet. Also liegen im Intervall
keine negativen Funktionswerte vor.
. Der Graph ist eine nach unten
geöffnete Parabel, die die x-Achse bei –3 bzw. 3 schneidet. Also liegen im Intervall
keine negativen Funktionswerte vor.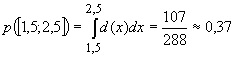
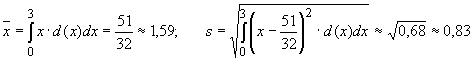
Lösungen der Aufgaben zu Durchschnitt, Standardabweichung und Normalverteilung
Lösung zu Aufgabe 1:
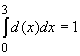 . Der Graph ist eine nach unten
geöffnete Parabel, die die x-Achse bei –3 bzw. 3 schneidet. Also liegen im Intervall
keine negativen Funktionswerte vor.
. Der Graph ist eine nach unten
geöffnete Parabel, die die x-Achse bei –3 bzw. 3 schneidet. Also liegen im Intervall
keine negativen Funktionswerte vor.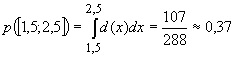
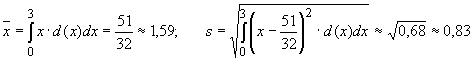
Lösung zu Aufgabe 3:
Die Dichtefunktion hat in dieser Aufgabe die Gleichung 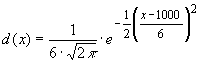 .
.
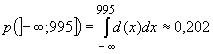 . Rund 20% der Tüten enthalten weniger als 995 g Zucker.
. Rund 20% der Tüten enthalten weniger als 995 g Zucker.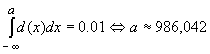 .
.
Die Werte der Integrale wurden mit DERIVE bestimmt. Es ist sinnvoll, den allgemeinen Funktionsterm der Normalverteilung in einer Datei zu speichern und bei jeder Aufgabe mit Hilfe der Parameter ‚Dichte‘ und Standardabweichung‘ anzupassen:
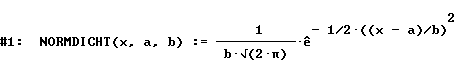
Bei Integralen, wie sie in dieser Aufgabe vorkommen, empfiehlt es sich, zunächst eine exakte Vereinfachung durchzuführen und erst danach zu approximieren. Will man direkt den Wert des Integrales approximieren, benötigt DERIVE erheblich mehr Zeit dafür.
Bei Gleichungen, wie sie in Teil b) vorkommen, kann eine exakte Lösung nicht erfolgen. Deshalb sind solche Gleichungen nummerisch zu lösen. Die Lösung ist sicherlich kleiner als der Mittelwert. Daher kann das Intervall, in dem das Programm die Lösung suchen soll, leicht angegeben werden.
Lösung mit Hilfe von DERIVE (als Bild)
Download der komprimierten DERIVE-Dateien (Normdichte, Aufgabe 3, Aufgabe 4)
Lösung zu Aufgabe 4:
Die Dichtefunktion für die Teile a) und b) hat die Gleichung 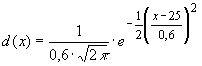 .
.
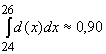 . Somit weicht bei rund 90% der Nägel die
Länge weniger als 1 mm vom Soll-Wert ab.
. Somit weicht bei rund 90% der Nägel die
Länge weniger als 1 mm vom Soll-Wert ab.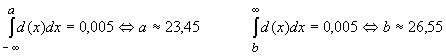 .
.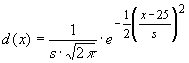 .
. 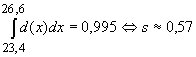 .
.
Lösung mit Hilfe von DERIVE (als Bild)
Download der komprimierten DERIVE-Dateien (Normdichte, Aufgabe 3, Aufgabe 4)