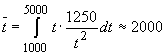Die Lebensdauer von Fernsehbildröhren eines bestimmten Typs kann durch die Dichtefunktion mit der Gleichung
beschrieben werden. Gesucht ist die durchschnittliche Lebensdauer.
Stunde 10 ; Doppelstunde 11/12: Durchschnitt bei stetigen Zufallsgrößen
Aufgabe: (nach LS, S.192)
Die Lebensdauer von Fernsehbildröhren eines bestimmten Typs kann durch die Dichtefunktion mit der Gleichung
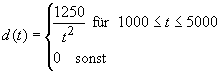
beschrieben werden. Gesucht ist die durchschnittliche Lebensdauer.
Der Durchschnittswert ist mit den bisher bekannten Methoden nicht zu bestimmen, da es unendlich viele mögliche Werte gibt. Ausgangspunkt zur Entwicklung einer neuen Methode ist die bekannte Durchschnittsberechnung bei endlich vielen diskreten Werten:
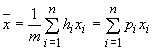, wobei die möglichen Werte 
jeweils die Häufigkeit 
haben und insgesamt 
Ergebnisse vorliegen.
Das läßt sich zunächst auf stückweise konstante Dichtefunktionen verallgemeinern:
Durch den Graphen sei eine Dichtefunktion im Intervall [0;50] gegeben.
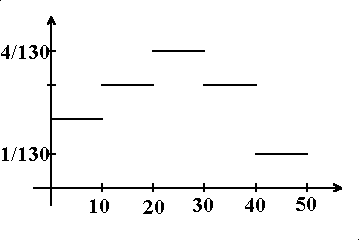
Es ist zwar die Wahrscheinlichkeit für ein Intervall berechenbar, aber es gibt immer noch unendlich viele Werte im Intervall. Betrachte zunächst nur das Intervall von 0 bis 10. Wegen der konstanten Dichte ist kein Wert in diesem Intervall bevorzugt. Der Durchschnitt, gebildet über alle Werte dieses Intervalls, ist also 5. Somit läßt sich wie folgt argumentieren:
Ein Wert zwischen 0 und 10 tritt mit der Wahrscheinlichkeit 
auf d. h. im Durchschnitt tritt der Wert 5
mit der Wahrscheinlichkeit 
auf.
Entsprechen läßt sich für die anderen Abschnitte mit konstanter Dichte argumentieren:
Im Durchschnitt tritt der Wert 15 mit der Wahrscheinlichkeit 
auf.
.....
Im Durchschnitt tritt der Wert 45 mit der Wahrscheinlichkeit 
auf.
Das Problem ist damit zurückgeführt auf endlich viele Werte:
, wobei
.
Konkret ergibt sich für die Beispielfunktion der Mittelwert:
Beim Übergang zur kontinuierlichen Dichtefunktion muss die Multiplikation verallgemeinert werden:
.
Somit ergibt sich für die durchschnittliche Lebendauer der Bildröhre: 